Soutien Scolaire Gratuit !!!

[Maski]

Bah j'avais seulement l'équation en fait dans mon exercice.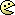
En tout cas merci.

[Maski]

Quelqu'un pourrait m'expliquer pourquoi, pour k allant de 0 à n, somme de (e^ix)^k = (1-(e^(ix))^(n+1))/((1-e^(ix)) ?

[Pod607]

Somme de termes d'une suite géométrique?

Allez salut

[Maski]

J'avais oublié cette formule, merci. Et je sais que je pose des questions un peu débiles parfois mais avec mon prof' de bases de l'analyse c'est vraiment pas évident de comprendre, même quelque chose de simple et de déjà vu au lycée.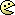

[Telanocx]

Je sais pas si ce topic est vraiment à jour,mais je post quand même (Je suis en 2nde,et une vraie brelle en Maths)

Je suis censé trouver une formule pouvant faire la somme des nombres impairs de 1 à 99.
Donc : 1+3+5+7+9+...+99 = ?
Voila,donc si quelqu'un pouvait m'aider,ça serait très gentil de sa part

[newbie]

Essayes d’additionner le premier nombre avec le dernier, puis le deuxième avec l'avant-dernier, etc

[lugiaI]

Comme il s'agit des cinquante premiers nombres impairs, ne suffit-il pas de faire 50 au carré ? Ce qui au passage fait 2500
Pour additionner des nombres impairs, s'ils se suivent à partir de 1, il faut multiplier le nombre de nombres impairs par lui-même, je sais pas si je suis clair...

[Telanocx]

Donc si je suis bien ton raisonnement,je suis censé faire 99²,c'est ca ?

[lugiaI]

Non, ce n'est pas ce que j'ai dit :

Comme il s'agit des cinquante premiers nombres impairs, ne suffit-il pas de faire 50 au carré ? Ce qui au passage fait 2500
Pour additionner des nombres impairs, s'ils se suivent à partir de 1, il faut multiplier le nombre de nombres impairs par lui-même, je sais pas si je suis clair...

Si tu avais seulement "1+3+5+7+9", comme il y a cinq chiffres, il faudrait faire 5 au carré, donc 5*5=25. Si tu avais "1+3+5+7+9+11+13+15+17+19", il faudrait faire le nombre de nombres (10) au carré donc 10*10=100.
Comme dans ton cas il y a cinquante nombres impairs, il faut faire 50*50=2500

[Telanocx]

Donc si j'ai bien compris,entre 1 et 99,il y a 50 nombres impairs ( J'ai cru que c'était 48),et je dois multiplier la somme des nombres impairs consécutifs présents entre 1 et 99 par lui même,donc au carré ? (Oui,je suis vraiment bête,j'arrive pas à comprendre)

[Pod607]

Réécris l'addition comme ça :

1 + 3 + 5 + 7 + ... +49
+
99 + 97 + 95 + 93 + ... + 51
=
100 + 100 + 100 + 100 + ... + 100

Si tu fais chaque somme en hauteur, tu tombes sur 100.
Et le nombre de fois que tu as 100 dans la somme finale, c'est aussi le nombre de nombres impairs de 1 à 49 (Il y en a 25, tu peux les compter)
Donc ta somme totale c'est 25 * 100 = 2500

[lugiaI]

C'est ça, tu as cinquante nombre impairs entre 1 et 99 compris, donc puisqu'ils sont consécutifs, tu peux faire cinquante au carré.
Et l'autre explication bien que plus longue tient aussi, car cinquantn au carré ou vingt-cinq fois cent font tous deux deux-milles-cinq-cent.

[Maski]

On pouvait pas faire moyenne des termes extrêmes x nombre de termes aussi ?

[newbie]

La formule générale pour la somme des termes d'une suite arithmétique, avec n le rang est ((u1+un)/2)*n
Or ta suite est la suite arithmétique de raison 2 et de premier terme 1
Donc en gros oui

[Pod607]

Il est en seconde kek

[newbie]

Mais Maski non

[Maski]

Mais pourquoi on ne peut pas appliquer la formule ((u1+un)/2)*n ?

[Pod607]

Bien sûr que si on peut, ça fait (1+99)/2 * 50 = 2500

[Maski]

Ah c'est bien ce que je me disais.

[Khimeira]

En fait ce qu'il essaie de te faire comprendre, Maski, c'est que ta réponse est correcte mais c'est pas ce qu'on attend